파티션 문제는 list 의 원소들을 합이 같은 두 개의 부분 집합으로 나눌 수 있지를 확인하는 문제입니다.
Example
예를 들어 아래와 같은 리스트가 있다면,
[1, 5, 11, 5]
리스트를 아래와 같이 나누게 되면, 두 리스트의 합이 11로 같기 때문에, 결과는 True가 됩니다.
[1, 5, 5], [11]
Recursion 을 이용한 풀이
Recursion 을 이용할 때는, subset에 대한 합계를 체크하는 method를 정의해서 subset 합계가 전체 원소의 합의 절반이 되면 True를 리턴하게 작성합니다.
def isSubsetSum(arr, n, target):
# Termination Cases
if target == 0:
return True
if n == 0 and target != 0:
return False
# exclude last element or include last element
return isSubsetSum(arr, n-1, target) or isSubsetSum(arr, n-1, target-arr[n-1])
def findPartition(arr):
total = sum(arr)
if total % 2 != 0:
return False
return isSubsetSum(arr, len(arr), total // 2)
assert(findPartition([1,2,3,4,5]) == False)
assert(findPartition([1,5,11,5]) == True)
assert(findPartition([1,2,3,4,4,3,2,1]) == True)
이 경우, 시간 복잡도는 O(2^N) 이 되며, 공간 복잡도는 O(N) 이 됩니다.
Recursion 을 이용한 풀이 2 - memoization
Recursion 을 이용할 때는, subset sum 을 확인하는 과정에서 반복되는 계산이 나오기 때문에, 이를 기록해 두고 사용하면 반복 계산을 크게 줄일 수 있습니다. memoization 기법을 사용하여 개선한 코드는 다음과 같습니다.
def isSubsetSum(arr, n, target, dp):
# Termination Cases
if target == 0:
return True
if n == 0 and target != 0:
return False
# send result from memo
if dp[n][target] != -1:
return dp[n][target]
# save result
dp[n][target] = isSubsetSum(arr, n-1, target, dp) or isSubsetSum(arr, n-1, target-arr[n-1], dp)
# return result
return dp[n][target]
def findPartition(arr):
total = sum(arr)
if total % 2 != 0:
return False
n = len(arr)
# init memoization result
dp = [[-1]*(total+1) for i in range(n+1)]
return isSubsetSum(arr, n, total // 2, dp)
assert(findPartition([1,2,3,4,5]) == False)
assert(findPartition([1,5,11,5]) == True)
assert(findPartition([1,2,3,4,4,3,2,1]) == True)
여기서는 테스트한 list의 아이템이 많지 않아서, Recursion 보다도 느린 결과가 나올 수 있지만, 원소가 증가할 수록 큰 성능 향상을 확인할 수 있을 것입니다.
Dynamic Programming 을 이용한 풀이
이번에는 합계 / 원소 테이블을 생성해서, 테이블의 값을 채워가는 방식으로 문제를 해결해 보도록 하겠습니다. 이 방식의 아이디어는 다음과 같습니다.
1. row에는 부분집합의 합계를, column에는 리스트의 원소를 하나씩 추가할 수 있게 테이블을 준비합니다.
[1, 3, 7, 3] 의 케이스를 예를 들면,
전체 원소의 합은 14 (1 + 3 + 7 + 3) 이기 때문에, 원소들의 합이 같게 나눴을 때, 부분 집합의 원소의 합은 7이 되어야 합니다. (전체 원소 합의 절반) 그러면, 테이블은 아래와 같이 준비 됩니다.
| [] | [1] | [1, 3] | [1, 3, 7] | [1, 3, 7, 3] | |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 |
2. 부분 집합의 합계가 0이라는 것은, 부분 집합이 공집합이면 언제나 가능하기 때문에 어떤 부분 집합의 부분 집합에 대해서도 합계 0을 만들 수가 있습니다. 그래서 첫 번째 줄은 모두 가능하기 때문에 True로 채웁니다.
| [] | [1] | [1, 3] | [1, 3, 7] | [1, 3, 7, 3] | |
| 0 | True | True | True | True | True |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 |
3. 반대로, 원소가 없는 부분집합에 대해서는 원소의 합계는 항상 0이기 때문에 합계가 0보다 큰 경우는 만드는 것이 불가능합니다. 따라서 첫 번째 컬럼은 False로 채웁니다.
| [] | [1] | [1, 3] | [1, 3, 7] | [1, 3, 7, 3] | |
| 0 | True | True | True | True | True |
| 1 | False | ||||
| 2 | False | ||||
| 3 | False | ||||
| 4 | False | ||||
| 5 | False | ||||
| 6 | False | ||||
| 7 | False |
4. 이제부터는 주어진 합계에 대해서, 원소를 채워가면서, 주어진 합계를 부분 집합의 합으로 만들 수 있는지를 체크합니다. 체크하는 방법은 마지막에 추가한 원소를 제외하고, 주어진 합계에서 해당 원소의 값을 뺀 경우에 대해서 부분 집합의 합을 만들 수 있는지를 체크하면 됩니다.
4-1. 먼저 부분 집합 [1] 의 부분 집합으로 합계 1을 만들 수 있는 지를 체크해 보겠습니다.
마지막에 추가한 원소는 "1" 이기 때문에, 해당 원소를 제거하고, 합계에서도 1을 뺍니다.
그러면, 부분 집합 []의 부분 집합으로 합계 0을 만들 수 있는 지를 체크해서, 그게 가능하면 부분 집합 [1]의 부분집합으로 합계 1을 만들 수 있는 지 알 수 있습니다. 우리는 이미 부분 집합 [] / 합계 0에 대해서 True로 채워 두었기 때문에 가능 하다는 것을 알 수 있습니다.
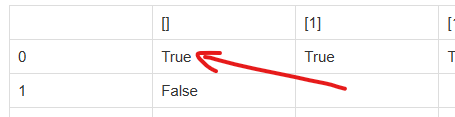
| [] | [1] | [1, 3] | [1, 3, 7] | [1, 3, 7, 3] | |
| 0 | True | True | True | True | True |
| 1 | False | True | |||
| 2 | False | ||||
| 3 | False | ||||
| 4 | False | ||||
| 5 | False | ||||
| 6 | False | ||||
| 7 | False |
4-2. 이번에는 부분 집합 [1, 3]의 부분 집합으로 합계 1을 만들 수 있는 지를 체크해 보겠습니다.
우리는 이미 부분 집합 [1]의 부분 집합으로 합계 1을 만들 수 있다는 것을 알고 있습니다. 그렇다면 [1]은 [1, 3]의 부분 집합이기 때문에, [1, 3]의 부분집합으로도 부분 집합의 합계 1을 만들 수 있습니다.

| [] | [1] | [1, 3] | [1, 3, 7] | [1, 3, 7, 3] | |
| 0 | True | True | True | True | True |
| 1 | False | True | True | ||
| 2 | False | ||||
| 3 | False | ||||
| 4 | False | ||||
| 5 | False | ||||
| 6 | False | ||||
| 7 | False |
5. 4번의 방법을 이용해서 테이블을 모두 채우면 아래와 같이 됩니다.
| [] | [1] | [1, 3] | [1, 3, 7] | [1, 3, 7, 3] | |
| 0 | True | True | True | True | True |
| 1 | False | True | True | True | True |
| 2 | False | False | False | False | False |
| 3 | False | False | True | True | True |
| 4 | False | False | True | True | True |
| 5 | False | False | False | False | False |
| 6 | False | False | False | False | True |
| 7 | False | False | False | True | True |
6. 원래 우리가 찾던 답이 [1, 3, 7, 3]의 부분 집합 중에 합이 7인 것이 있는 지를 찾는 것이 었기 때문에, 위의 테이블의 가장 오른쪽 아래의 값을 읽어서 돌려주면 됩니다.
설명은 길었지만, 코드는 기존의 recursion 보다 짧습니다.
def findPartition(arr):
total = sum(arr)
if total % 2 != 0:
return False
half_sum = total // 2
n = len(arr)
# table setting
dp = [[True]*(n+1)] + ([[False]*(n+1)] * half_sum)
# fill the table
for i in range(1, half_sum+1):
for j in range(1, n+1):
if dp[i][j-1]:
dp[i][j] = True
continue
val = arr[j-1]
if i >= j and dp[i-val][j-1]:
dp[i][j] = True
# return result
return dp[half_sum][n]
assert(findPartition([1,2,3,4,5]) == False)
assert(findPartition([1,5,11,5]) == True)
assert(findPartition([1,2,3,4,4,3,2,1]) == True)
Dynamic Programming 공간 최적화
마지막으로 바로 전에 사용한 Dynamic Programming을 최적화 해보도록 하겠습니다. 위의 테이블을 잘 살펴보면, 실제로는 전체 테이블이 없어도 한 컬럼만 가지고 정보를 업데이트하면서 사용이 가능합니다. 다만 이전 단계의 결과를 체크하기 위해서는 top-down 방식이 아닌 bottom-up 방식으로 리스트를 채워가야 합니다.
1. 먼저 전체 리스트 원소의 합계의 절반 크기의 리스트를 생성합니다. 인덱스는 부분 집합의 합계를 나타내기 때문에, 0은 True로 세팅하고 나머지는 False로 세팅합니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Initial | True | False | False | False | False | False | False | False |
2. 이번에는 원소를 하나씩 추가해가며, 합계를 제일 큰 수부터 순차적으로 체크해서 리스트를 업데이트 해줍니다.

체크는 다음과 같이 할 수 있습니다.
2-1. 해당 합계를 이미 만들 수 있다면 continue (dp[j] = True 인 경우)
2-2. 해당 합계에서 추가한 원소의 값을 뺀 값을 부분 집합의 합으로 만들 수 있는지를 체크해서 True인 경우, 해당 합계를 True로 업데이트 (dp[j - val] = True 인 경우)
ex)
첫번째 원소 1 추가
합계 7에서부터 역순으로 합계 0까지 체크
합계 7의 경우 현재 False 이기 때문에, dp[7-1] 에 있는 값을 체크
=> 현재 dp[6] = False 이기 때문에 업데이트를 하지 않고 진행
...
합계 1의 경우 현재 False 이기 때문에, dp[1-1]에 있는 값을 체크
=> 현재 dp[0] = True 이기 때문에 dp[1] = True로 업데이트
합계 0의 경우 이미 True 이기 때문에 continue
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| [1] | True | True | False | False | False | False | False | False |
3. 순차적으로 원소를 추가하며 테이블을 업데이트 해주면.. 아래와 같이 업데이트 됩니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| [1, 3] | True | True | False | True | True | False | False | False |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| [1, 3, 7] | True | True | False | True | True | False | False | True |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| [1, 3, 7, 3] | True | True | False | True | True | False | True | True |
4. 리스트의 마지막 값인 dp[7] 을 읽어서 돌려 줍니다.
코드로 구현하면 다음과 같습니다.
def findPartition(arr):
total = sum(arr)
if total % 2 != 0:
return False
half_sum = total // 2
n = len(arr)
# init list
dp = dp = [True] + [False] * half_sum
# update list
for i in range(n):
val = arr[i]
for j in range(half_sum, val-1, -1):
if dp[j]:
continue
if dp[j-val] == True:
dp[j] = True
# return result
return dp[half_sum]
assert(findPartition([1,2,3,4,5]) == False)
assert(findPartition([1,5,11,5]) == True)
assert(findPartition([1,2,3,4,4,3,2,1]) == True)
실제로, 위의 코드에서 dp[half_sum] = True 가 되는 순간, 더 이상 for 문을 수행할 필요 없이 True를 돌려줘도 됩니다.
여기서는 이전 단계의 합계를 참조하기 위해서 bottom-up (가장 큰 합계를 먼저 체크) 하는 방식을 사용하였습니다.
DP 에서는 어떤 방향으로 테이블 혹은 리스트를 채우냐에 따라 공간 복잡도를 더 작게 구현할 수 있습니다.