코드노예

피보나치 수는 첫째 및 둘째 항이 1이며, 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열로 정의되어 있습니다.

경우에 따라 0번째 항의 값을 0으로 정의하기도 합니다.

피보나치 수를 0번째부터 시작하여 20개를 나열하면 다음과 같습니다.

피보나치 수에 대해서 자세한 내용을 알고 싶으신 분은 아래 링크를 참고하시기 바랍니다.

https://en.wikipedia.org/wiki/Fibonacci_sequence#Primes_and_divisibility

한글 위키 페이지도 있으나.. 내용이 조금 부실한 편이라 영문 위키 페이지를 링크로 달았습니다.

Recursion 을 이용한 풀이

위의 정의대로 Python을 이용해서 구현해 보면, 대략 다음과 같은 코드로 구현이 가능합니다.

def fibo(n):
    if n < 1:
        return 0
    elif n < 3:
        return 1
    return fibo(n-1) + fibo(n-2)

fibo(19)를 출력해보면, 4181이 나오는 것을 확인할 수 있습니다.

Memoization 을 이용한 성능 개선

Recursion 을 이용하여 구현한 코드는 중복된 계산이 많아서 퍼포먼스에 문제가 있습니다. 

fibo(5) 를 구하기 위해서 fibo(4) + fibo(3) 이 호출되고,

fibo(4) 를 구하기 위해서 다시 fibo(3) + fibo(2) 가 호출되고..

같은 계산을 여러 번 중복하는 것을 기록해 두어 성능을 개선해 보겠습니다. 아래 코드는 memoization 을 이용하여 성능을 개선한 코드입니다.

mCache = {}
mCache[1] = 1
mCache[2] = 1

def fibo_memo(n):
    if n in mCache:
        return mCache[n]
    elif n < 1:
        return 0
    ret = fibo_memo(n-1) + fibo_memo(n-2)
    mCache[n] = ret
    return ret

한 번 계산을 했던 값은 mCache에 값을 기록해 두어, 중복 계산을 피해서 퍼포먼스를 향상시켰습니다.

Dynamic Programming 을 이용한 풀이

이번에는 테이블을 생성해서 값을 채워가는 방식으로 피보나치 값을 계산해 보겠습니다.

def fibo_dp(n): 
    if n < 1:
        return 0
    
    buf = [0] * (n+1)
    buf[1] = 1
    for i in range(2, n+1):
        buf[i] = buf[i-1] + buf[i-2]
    return buf[n]

피보나치 수열의 정의대로 순차적으로 계산해서 마지막 값을 돌려줍니다. 

Dynamic Programming 개선

위에서 살펴본 Dynamic Programming에서는 테이블을 이용하였기 때문에, n+1 만큼의 메모리를 할당해서 값을 구하였습니다. 하지만 실제로는 이전의 계산 결과는 더 이상 쓰이지 않기 때문에, 이전값, 현재값을 가지고 있는 것으로 충분합니다. 위의 코드는 아래와 같이 개선이 가능합니다.

def fibo_dp2(n): 
    if n < 1:
        return 0
    
    prev = 0
    current = 1
    for i in range(1, n):
        prev, current = current, prev + current
    return current

Matrix를 이용한 풀이

마지막으로 matrix를 이용하여 피보나치 값을 구해 보도록 하겠습니다.

피보나치 수열은 행렬을 이용하면 다음과 같이 정의가 가능합니다.

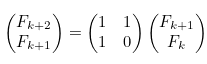
위의 행렬을 두 개 붙여서 확장하면, 다음과 같은 식을 얻을 수 있습니다.

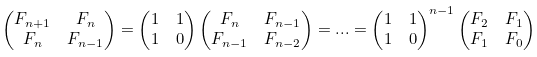
F0 ~ F2에 값을 대입해서, 식을 정리해 보면 다음과 같습니다. 

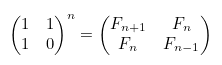
즉, Fn 을 구하기 위해서는 아래 행렬의 (0,0) 값을 계산하면 됩니다.

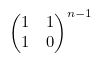
행렬식의 계산은 다음과 같이 처리합니다.

1) 지수가 짝수인 경우,

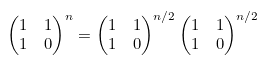
2) 지수가 홀수인 경우,

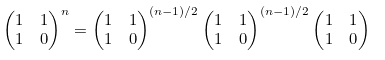
위의 내용을 코드로 구현하면 다음과 같습니다.

def calc_matrix(m1, m2):
    e00 = m1[0][0] * m2[0][0] + m1[0][1] * m2[1][0]
    e01 = m1[0][0] * m2[0][1] + m1[0][1] * m2[1][1]
    e10 = m1[1][0] * m2[0][0] + m1[1][1] * m2[1][0]
    e11 = m1[1][0] * m2[0][1] + m1[1][1] * m2[1][1]
    return [[e00, e01], [e10, e11]]

mBase = [[1, 1], [1, 0]]    
def power(m, n):
    if n <= 1:
        return mBase
    ret = power(m, n//2)
    ret = calc_matrix(ret, ret)
    if n % 2 == 1:
        ret = calc_matrix(ret, mBase)
    return ret

def fibo_mat(n):
    if n < 1:
        return 0
    m = power(mBase, n-1)
    return m[0][0]

지수 형태로 구현하였기 때문에, 시간 복잡도는 O(logN) 이 됩니다.

퍼포먼스 비교

각 방법에 대해서 F1000 을 구했을 때 걸리는 시간을 측정한 결과입니다.

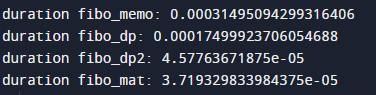
recursion 의 경우, 시스템에 따라 다를 수 있지만 일정 갯수 이상이 되면, maximum recursion depth exceeded 에러가 발생합니다. 

recursion 을 제외한 나머지에 대해서, F10000을 구했을 때 걸리는 시간을 측정한 결과 입니다.